Математика и изобразительное искусство

     Исторически, математика играла важную роль в изобразительном искусстве, в частности при изображении перспективы, подразумевающем реалистичное изображение трехмерной сцены на плоском холсте или листе бумаги. Согласно современным взглядам, математика и изобразительное искусство очень удаленные друг от друга дисциплины, первая - аналитическая, вторая - эмоциональная. Математика не играет очевидной роли в большинстве работ современного искусства, и, фактически, многие художники редко или вообще никогда не используют даже использование перспективы. Однако, есть много художников, у которых математика находится в центре внимания. Несколько значительных фигур в изобразительном искусстве проложили дорогу этим индивидуумам. 

     Вообще-то не существует каких-либо правил или ограничений на использование различных тем в математическом искусстве. Однако, есть несколько тем, которые достаточно часто различным художниками. Среди них есть использование многогранников, тесселяций, невозможных фигур, лент Мебиуса, искаженных или необычных систем перспективы, а также фракталов.

Многогранники

     Многогранник - это трехмерное тело, гранями которого являются многоугольники. Существует всего пять правильных многогранников, у которых все стороны являются правильными многоугольниками и все вершины одинаковы. Они известны как многоугольники Платона или Платоновы тела. Также существует 13 выпуклых многогранников, гранями которых являются один, два или три правильных многоугольника, и у которых все вершины одинаковы. Они известны как тела Архимеда. Кроме этого существует бесконечное множество призм и антипризм с гранями в виде правильных многоугольников. Эшер использовал многогранники во многих своих работах, включая "Рептилии" (1949), "Двойной планетоид" (1949) и "Гравитация" (1952).

Тесселляции

     Тесселляции, известные также как покрытие плоскости плитками (tiling), являются коллекциями фигур, которые покрывают всю математическую плоскость, совмещаясь друг с другом без наложений и пробелов. Правильные тесселляции состоят из фигур в виде правильных многоугольников, при совмещении которых все углы имеют одинаковую форму. Существует всего три многоугольника, пригодные для использования в правильных тесселляциях. Это - правильный треугольник, квадрат и правильный шестиугольник. Полуправильными тесселляциями называют такие тесселляции, в которых использованы правильные многоугольники двух или трех типов и все вершины одинаковы. Существует всего 8 полуправильных тесселляций. Вместе три правильных тесселляции и восемь полуправильных носят название Архимедовых. Тесселляции, в которых отдельные плитки являются узнаваемыми фигурами, являются одной из основных тем творчества Эшера. В его записных книгах содержатся более 130 вариантов тесселляций. Он использовал их в огромном количестве своих картин, среди которых "День и ночь" (1938), серия картин "Предел круга" I-IV, и знаменитые "Метаморфозы" I-III (1937-1968).

Вверху картина Hollister David "Семь птиц". На ней изображены семь птиц, две из которых изображены в негативе на фоне ландшафта города Ахо в Аризоне. Последовательно уменьшающиеся фигуры птиц совмещаются друг с другом в виде фрактальной тесселляции. Хвостовые перья каждой птицы являются разделяют конструкцию напополам, отсекая примерно треть расстояния между кончиками крыльев. Каждая меньшая птица в свою очередь делит свою область аналогичным образом. Если этот процесс продолжать до бесконечности, получится набор точек, известный как множество Кантора или Канторова пыль.

Невозможные фигуры

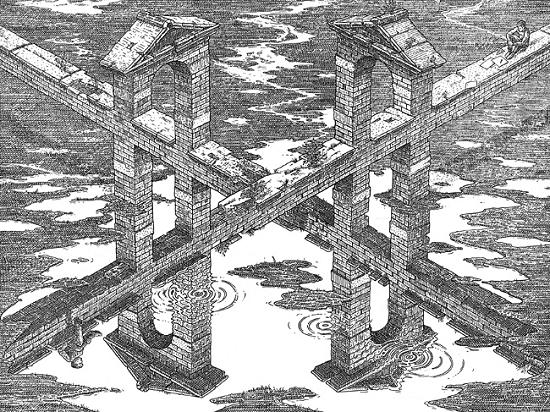     Невозможные фигуры - эти фигура, изображенная в перспективе таким способом, чтобы выглядеть на первый взгляд обычной фигурой. Однако при более внимательном рассмотрении зритель понимает, что такая фигура не может существовать в трехмерном пространстве. Эшер изобразил невозможные фигуры на своих известных картинах "Бельведер" (1958), "Восхождение и спуск" (1960) и "Водопад" (1961). Одним из примеров невозможной фигуры служит картина современного венгерского художника Иштвана Ороса (Istvan Orosz).

    Справа картина Istvan Orosz "Перекрестки" (1999). Репродукция гравюры по металлу. На картине изображены мосты, которые не могут существовать в трехмерном пространстве. Например, есть отражения в воде, которые не могут быть исходными мостами.

Лента Мебиуса

     Лента Мебиуса - это трехмерный объект, имеющий только одну сторону. Такая лента может быть легко получена из полоски бумаги, перекрутив один концов полоски, а затем склеив оба конца друг с другом. Эшер изобразил ленту Мебиуса на работах "Всадники" (1946), "Лента Мебиуса II (Красные мурвьи)" (1963) и "Узлы" (1965). 

      Позднее, поверхности минимальной энергии стали вдохновением для многих математических художников. Брент Коллинз (Brent Collins), использует ленты Мебиуса и поверхности минимальной энергии, а также другие виды абстракций в скульптуре.

Искаженные и необычные перспективы

     Необычные системы перспективы, содержащие две или три исчезающие точки, также являются излюбленной темой многих художников. К ним также относится родственная область - анаморфное искусство. Эшер использовал искаженную перспективу в нескольких своих работах "Наверху и внизу" (1947), "Дом лестниц" (1951) и "Картинная галерея" (1956). Дик Термес (Dick Termes) использует шеститочечную перспективу для рисования сцен на сферах и многогранниках, как показано на примере слева.

    Dick Termes "Клетка для человека" (1978). Это разукрашенная сфера, в процессе создания которой использовалась шеститочечная перспектива. На ней изображения геометрическая структура в виде сетки, сквозь которую виден ландшафт. Три ветки проникают внутрь клетки, а также по ней ползают рептилии. В то время как одни изучают мир, другие обнаруживают себя, находящимися в клетке.

     Слово анаморфный (anamorthic) сформировано из двух греческих слов "ana" (снова) и morthe (форма). К анаморфным относятся изображения настолько сильно искаженные, что разобрать их без специального зеркала бывает невозможно. Такое зеркало иногда называют анаморфоскопом. Если смотреть в анаморфоскоп, то изображение "формируется снова" в узнаваемую картину. Европейские художники раннего Ренессанса были очарованы линейными анаморфными картинами, когда вытянутая картина становилась снова нормальном при обзоре под углом. Известный премер - картина Ханса Хольбейна (Hans Holbein) "Послы" ("The Ambassadors") (1533), в которой изображен вытянутый череп. Картина может быть наклонена в верхней части лестницы так, что люди, поднимающиеся по лестнице будут напуганы изображением черепа. Анаморфные картины, для просмотра которых необходимы цилиндрические зеркала, были популярны в Европе и на Востоке в XVII-XVIII веках. Часто такие изображения несли сообщения политического протеста или были эротического содержания. Эшер не использовал в своей работе классические анаморфные зеркала, однако, в некоторых своих картинах он использовал сферические зеркала. Самая известная его работа в этом стиле "Рука с отражающей сферой" (1935). Пример ниже показывает классическое анаморфное изображение работы Иштвана Ороса (Isvan Orosz).

Фракталы

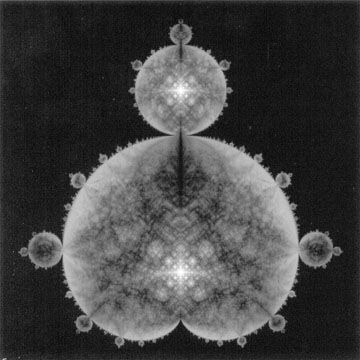    Фрактал - это объект, повторяющий сам себя в различных масштабах, которые связаны математическим способом. Фракталы формируются итерационно, многократно повторяя вычисления так, что получается объект высокой сложности с множеством мелких деталей. К сожалению, фракталы как таковые были недоступны Эшеру, потому что были формализованы и выделены в отдельную область математики лишь после его смерти. Эшер очень интересовался изображением бесконечного в пределах конечной области, в частности бесконечными тесселляциями. Он использовал сжимающиеся координатные сетки и гиперболическую геометрию для достижения этого эффекта, как показано в картинах "Предел круга" I-IV (1958-1960) и "Предел квадрата" (1964). Справа приведен пример современного художника Кэри Митчелл (Kerry Mitchell).

Kerry Mitchell "Будда" - компьютерная картина основанная на множестве Мандельброта, исследованного Бенуа Мандельбротом (Benoit Mandelbrot).

     Математические изобразительное искусство процветает сегодня, и многие художники создают картины в стиле Эшера и в своем собственном стиле. Эти художники работают в различных направлениях, включая скульптуру, рисование на плоских и трехмерных поверхностях, литографию и компьютерную графику. А наиболее популярными темами математического искусства остаются многогранники, тесселляции, невозможные фигуры, ленты Мебиуса, искаженные системы перспективы и фракталы.

Материал взят с сайта Невозможный мир